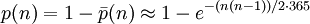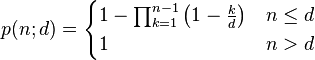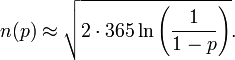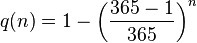티스토리 뷰

보안/일반

Birthday paradox - From Wikipedia, the free encyclopedia

NineKY 2007. 7. 13. 16:13

Birthday paradox

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In probability theory, the birthday paradox states that in a group of 23 (or more) randomly chosen people, there is more than 50% probability that some pair of them will have the same birthday. For 57 or more people, the probability is more than 99%, although it cannot be exactly 100% unless there are at least 366 people.[1] This is not a paradox in the sense of leading to a logical contradiction, but is called a paradox because mathematical truth contradicts naive intuition: most people estimate that the chance is much lower than 50%. Calculating the probabilities above (and related ones) is the birthday problem. The mathematics behind it has been used to devise a well-known cryptographic attack named the birthday attack.

Contents

[hide]

[edit] Understanding the paradox

One way to intuitively accept the birthday paradox is to realize that there are many possible unordered pairs of people whose birthdays could match. Specifically, among 23 people, there are C(23,2) = 23 × 22/2 = 253 pairs, each of which is a potential candidate for a match. Looked at in this way, it doesn't seem so unlikely that one of these 253 pairs yields a match.

The key to understanding this problem is to think about the chances of no two people sharing a birthday: what are the chances that person 1 has a different birthday from person 2 and that person 3 has a different birthday again and person 4, etc. As you add each person to the room, it becomes less and less likely that their birthday isn't already taken by someone else. If one has a sample space of n people, the first person has 365 possible birthdays to choose from. The 2nd person would have only 364, the 3rd would have 363, and so on and so forth. This would be compared with any person being able to have any birthday with no restrictions (in short, all people have 365 possible birthdates.) This leads to the equation below.

The actual birthday problem is asking if any of the 23 people have a matching birthday with any of the others — not one in particular. (See "Same birthday as you" below for an analysis of this much less surprising alternative problem.)

[edit] Calculating the probability

To compute the approximate probability that in a room of n people, at least two have the same birthday, we disregard variations in the distribution, such as leap years, twins, seasonal or weekday variations, and assume that the 365 possible birthdays are equally likely. Real-life birthday distributions are not uniform since not all dates are equally likely.[2]

It is easier to first calculate the probability p(n) that all n birthdays are different. If n > 365, by the pigeonhole principle this probability is 0. On the other hand, if n ≤ 365, it is given by

\bar p(n) = 1 \cdot \left(1-\frac{1}{365}\right) \cdot \left(1-\frac{2}{365}\right) \cdots \left(1-\frac{n-1}{365}\right) = { 365 \cdot 364 \cdots (365-n+1) \over 365^n } = { 365! \over 365^n (365-n)!}

because the second person cannot have the same birthday as the first (364/365), the third cannot have the same birthday as the first two (363/365), etc.

The event of at least two of the n persons having the same birthday is complementary to all n birthdays being different. Therefore, its probability p(n) is

p(n) = 1 - \bar p(n) .

This probability surpasses 1/2 for n = 23 (with value about 50.7%). The following table shows the probability for some other values of n (This table ignores the existence of leap years, as described above):

n p(n)
10 12%
20 41%
23 50.7%
30 70%
50 97%
100 99.99996%
200 99.9999999999999999999999999998%
300 (1 − 7×10−73) × 100%
350 (1 − 3×10−131) × 100%
366 100%

[edit] Approximations

The Taylor series expansion of the exponential function

e^x = 1 + x + \frac{x^2}{2!}+\cdots
A graph showing the accuracy of the approximation 1 − exp(−n2/(2⋅365)).
A graph showing the accuracy of the approximation 1 − exp(−n2/(2⋅365)).

provides a first-order approximation for ex:

e^x \approx 1 + x

The first expression derived for p(n) can be approximated as

\bar p(n) \approx 1 \cdot e^{-1/365} \cdot e^{-2/365} \cdots e^{-(n-1)/365}
= 1 \cdot e^{-(1+2+ \cdots +(n-1))/365}
= e^{-(n(n-1))/2 \cdot 365}

Therefore,

p(n) = 1-\bar p(n) \approx 1 - e^{-(n(n-1))/2 \cdot 365}

An even coarser approximation is given by

p(n)\approx 1-e^{-n^2/{2 \cdot 365}},\,

which, as the graph illustrates, is still fairly accurate.

[edit] A simple exponentiation

Very basically, the probability of any two people not having the same birthday is 364/365. In a room of people of size N, there are C(N, 2) pairs of people, i.e. C(N, 2) events. We can approximate the probability of no two people sharing the same birthday by assuming that these events are independent and hence by multiplying their probability together. In short we multiply 364/365 by itself C(N, 2) times, which gives us

\left(\frac{364}{365}\right)^{C(N,2)}

And obviously if this is the probability of no one having the same birthday, then the probability of someone sharing a birthday is

p(n)\approx 1 - \left(\frac{364}{365}\right)^{C(N,2)}.

[edit] Poisson approximation

Using the Poisson approximation for the binomial,

\mathrm{Poi}\left(\frac{C(23, 2)}{365}\right) \approx \mathrm{Poi}\left(\frac{253}{365}\right) \approx \mathrm{Poi}(0.6932)
\Pr(X>0)=1-\Pr(X=0)=1-e^{-0.6932}=1-0.499998=0.500002.

Again, this is over 50%.

[edit] Approximation of number of people

We can also approximate this using the following formula for the number of people necessary to have at least a 50% chance of matching:

N = \frac{1}{2} + \sqrt{\frac{1}{4} + 2 \times 365 \times \ln(2)} \approx 22.9999

This is a result of the good approximation that an event with 1 in k probability will have a 50% chance of occurring at least once if it is repeated k ln 2 times.

[edit] An upper bound and a different perspective

The argument below is adapted from an argument of Paul Halmos.[3]

As stated above, the probability that no two birthdays coincide is

1-p(n) = \bar p(n) = \prod_{k=1}^{n-1}\left(1-{k \over 365}\right) .

We are interested in the smallest n such that p(n) > 1/2; or equivalently, the smallest n such that p(n) < 1/2.

Replacing 1 − k/365, as above, with e−k/365, and using the inequality 1 − x < e−x, we have

\bar p(n) = \prod_{k=1}^{n-1}\left(1-{k \over 365}\right) < \prod_{k=1}^{n-1}\left(e^{-k/365}\right) = e^{-(n(n-1))/(2\cdot 365)} .

Therefore, the expression above is not only an approximation, but also an upper bound of p(n). The inequality

e^{-(n(n-1))/(2\cdot 365)} < \frac{1}{2}

implies p(n) < 1/2. Solving for n we find

n^2-n > 2\cdot365\ln 2 \,\! .

Now, 730 ln 2 is approximately 505.997, which is barely below 506, the value of n2 − n attained when n = 23. Therefore, 23 people suffice.

Note that the derivation only shows that at most 23 people are needed to ensure a birthday match with even chance; it leaves open the possibility that, say, n = 22 could also work.

[edit] Generalization

The birthday problem can be generalised as follows: given n random integers drawn from a discrete uniform distribution with range [1,d], what is the probability p(n;d) that at least two numbers are the same?

The generic results can be derived using the same arguments given above.

p(n;d) = \begin{cases} 1-\prod_{k=1}^{n-1}\left(1-{k \over d}\right) & n\le d \\ 1 & n > d \end{cases}
p(n;d) \approx 1 - e^{-(n(n-1))/2d}
q(n;d) = 1 - \left( \frac{d-1}{d} \right)^n
n(p;d)\approx \sqrt{2d\ln\left({1 \over 1-p}\right)}

[edit] Applications

The birthday paradox in its more generic sense applies to hash functions: the expected number of N-bit hashes that can be generated before getting a collision is not 2N, but rather only 2N/2. This is exploited by birthday attacks on cryptographic hash functions and is the reason why a small number of collisions in a hash table are, for all practical purposes, inevitable.

The theory behind the birthday problem was used in [Schnabel 1938] under the name of capture-recapture statistics to estimate the size of fish population in lakes.

[edit] Other birthday problems

[edit] Reverse problem

For a fixed probability p:

  • Find the greatest n for which the probability p(n) is smaller than the given p, or
  • Find the smallest n for which the probability p(n) is greater than the given p.

An approximation to this can be derived by inverting the 'coarser' approximation above:

n(p)\approx \sqrt{2\cdot 365\ln\left({1 \over 1-p}\right)}.

[edit] Sample calculations

p n n↓ p(n↓) n↑ p(n↑)
0.01 0.14178√365 = 2.70864 2 0.00274 3 0.00820
0.05 0.32029√365 = 6.11916 6 0.04046 7 0.05624
0.1 0.45904√365 = 8.77002 8 0.07434 9 0.09462
0.2 0.66805√365 = 12.76302 12 0.16702 13 0.19441
0.3 0.84460√365 = 16.13607 16 0.28360 17 0.31501
0.5 1.17741√365 = 22.49439 22 0.47570 23 0.50730
0.7 1.55176√365 = 29.64625 29 0.68097 30 0.70632
0.8 1.79412√365 = 34.27666 34 0.79532 35 0.81438
0.9 2.14597√365 = 40.99862 40 0.89123 41 0.90315
0.95 2.44775√365 = 46.76414 46 0.94825 47 0.95477
0.99 3.03485√365 = 57.98081 57 0.99012 58 0.99166

Note: some values falling outside the bounds have been coloured to show that the approximation is not always exact.

[edit] Same birthday as you

Comparing p(n) = probability of a birthday match with q(n) = probability of matching your birthday
Comparing p(n) = probability of a birthday match with q(n) = probability of matching your birthday

Note that in the birthday problem, neither of the two people are chosen in advance. By way of contrast, the probability q(n) that someone in a room of n other people has the same birthday as a particular person (for example, you), is given by

q(n) = 1 - \left( \frac{365-1}{365} \right)^n

Substituting n = 23 gives about 6.1%, which is less than 1 chance in 16. For a greater than 50% chance that one person in a roomful of n people has the same birthday as you, n would need to be at least 253. Note that this number is significantly higher than 365/2 = 182.5: the reason is that it is likely that there are some birthday matches among the other people in the room.

[edit] 365 different birthdays

How many people do you need to meet, in order to meet a person for each possible birthday? Intuitively, this number will be much higher than 365, but how much? (This problem is a special case of the Coupon collector problem.)

After having met people with n different birthdays (n < 365), the chance that the next person you meet has a colliding birthday is \frac{365-n}{365}. If the birthdays are distributed uniformly, this means that you will have to meet \frac{365}{365-n} people on average to find one with the a new birthday. This means that, on average and if you meet a person per day, it will take a year to find the person with the last missing birthday.

The total number of people to meet is then \sum_{n=0}^{364} \frac{365}{365-n}, or 2364.64 people.

The same reasoning applies in the following generalized problem: how many objects, belonging to one of d possible groups, do you have to collect in order to have one for each group? The answer is, on average,

\sum_{n=0}^{d-1} \frac{d}{d-n} = d \sum_{n=1}^{d} \frac{1}{n} = d H_d

where Hd is the d-th harmonic number.

[edit] Near matches

Another generalization is to ask how many people are needed in order to have a better than 50% chance that two people have a birthday within one day of each other, or within two, three, etc., days of each other. This is a more difficult problem and requires use of the inclusion-exclusion principle. The number of people required so that the probability that some pair will have a birthday separated by fewer than k days will be higher than 50% is:

k # people required
1 23
2 14
3 11
4 9
5 8
6 8
7 7
8 7

Thus in a group of just seven random people, it is more likely than not that two of them will have a birthday within a week of each other.[4]

[edit] Collision counting

The probability that the kth integer randomly chosen from [1, d] will repeat at least one previous choice equals q(k − 1;d) above. The expected total number of times a selection will repeat a previous selection as n such integers are chosen equals

\sum_{k=1}^n q(k-1;d) = n - d + d \left (\frac {d-1} {d} \right )^n.

[edit] References

  • Zoe Emily Schnabel: "The estimation of the total fish population of a lake", American Mathematical Monthly 45 (1938), pages 348-352
  • M. Klamkin and D. Newman: "Extensions of the birthday surprise", Journal of Combinatorial Theory 3 (1967), pages 279-282.
  • D. Bloom: "A birthday problem", American Mathematical Monthly 80 (1973), pages 1141-1142. This problem solution contains a proof that the probability of two matching birthdays is least for a uniform distribution of birthdays.

[edit] Notes

  1. ^ It is possible that a group of 366 people all have different birthdays, if one of the birthdays is February 29; then the probability that two are the same is 100% only when there are at least 367 people in the group. Also, birthdays are not evenly distributed throughout the year; not only does February 29 occur significantly less than any other day, but birth rates vary for the other 365 days. To keep things simple, all calculations in this article presume that there are 365 days in every year, and that birthdays are evenly distributed among those days. This will cause all these calculations to be very slightly wrong, but they are sufficiently accurate for the purpose of illustration.
  2. ^ In particular, many children are born in the summer, especially the months of August and September (for the northern hemisphere) [1], and in the U.S. it has been noted that many children are conceived around the holidays of Christmas and New Year's Day; and, in environments like classrooms where many people share a birth year, it becomes relevant that due to the way hospitals work, where C-sections and induced labor are not generally scheduled on the weekend, more children are born on Mondays and Tuesdays than on weekends. Both of these factors tend to increase the chance of identical birth dates, since a denser subset has more possible pairs (in the extreme case when everyone was born on three days, there would obviously be many identical birthdays). The birthday problem for such non-constant birthday probabilities was tackled by Murray Klamkin in 1967.
  3. ^ In his autobiography, Halmos criticized the form in which the birthday paradox is often presented, in terms of numerical computation. He believed that it should be used as an example in the use of more abstract mathematical concepts. He wrote:

    The reasoning is based on important tools that all students of mathematics should have ready access to. The birthday problem used to be a splendid illustration of the advantages of pure thought over mechanical manipulation; the inequalities can be obtained in a minute or two, whereas the multiplications would take much longer, and be much more subject to error, whether the instrument is a pencil or an old-fashioned desk computer. What calculators do not yield is understanding, or mathematical facility, or a solid basis for more advanced, generalized theories.

  4. ^ Abramson, M.; Moser, W. O. J. (1970). "More Birthday Surprises". American Mathematical Monthly 77: pp. 856-858. 

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Birthday_paradox"

'보안 > 일반' 카테고리의 다른 글

Broad Spectrum of Network Threat  (0) 2007.12.22
[해커스쿨] chenkim4의 네비게이션 해킹? 편 (펌)  (0) 2007.09.09
Understanding 802.11 Frame Types  (0) 2007.07.06
KLDP Code Fest/KSP  (0) 2007.07.06
NHN-KISA, 악성코드 은닉사이트 탐지 협력  (0) 2007.07.06
공지사항
최근에 올라온 글
최근에 달린 댓글
Total
Today
Yesterday
링크
TAG more
«   2024/04   »
일 월 화 수 목 금 토
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30
글 보관함